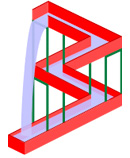
This Escher-like diagram illustrates a figure that expresses the infinite, which Maharishi has said is the goal for both a scientist and an artist.

Infinity on the page, the geometric art of M C Escher
by Global Good News staff writer
8 July 2010

In a series entitled ‘Consciousness: The Inside Story,’ on KHOE, the university radio station of Maharishi University of Management, in Fairfield, Iowa, USA, Dr Cathy Gorini, Chair of the Department of Mathematics at the university, presented an excerpt from her undergraduate mathematics course ‘Geometry for Artists’. In 2001 Dr Gorini received the Outstanding College Teaching Award from the Mathematical Association of America.  

In her talk Dr Gorini said that someone had once asked Maharishi what is the goal of an artist and what is the goal of a scientist? Maharishi had answered that for both the scientist and the artist the goal is the same; the goal will always be the same. The goal is infinity. 

Maharishi had that said the goal of the artist is to express the infinite. ‘If one thinks about what an artist wants to do,’ Dr Gorini continued, ‘they have something inside that they want to communicate to somebody else. They are expressing something—and the deepest value of what they are expressing is infinity.’  

An artist may be expressing other things, ‘but what makes art charming and why you want to keep looking at it, is that there's something very deep there,’ she said. ‘There's something, we could say even infinite, about it. The artist can express whatever value of infinity they have experience or knowledge of.’ 

Dr Gorini explained that a scientist is always probing for more and more knowledge. In mathematics we find that knowledge is always about the infinite. ‘Even if you are studying triangles,’ she said, ‘and you say “Well, a triangle is this finite shape,” the mathematician says, “Yes, but there's infinitely many triangles and I want to know about every single triangle.”’ 

The way the mathematician can help the artist is that the artist wants to express infinity but there are two things: the artist may want to learn more about infinity and the artist may want techniques for expressing infinity. The artist M C Escher is a beautiful example, Dr Gorini said, because he worked with mathematicians to understand more of the different ideas in geometry. ‘With these ideas he wanted to find a way to express infinity,’ she said. 

Dr Gorini read a quote from Escher that shows this—'From the first time I dared to work on the problem of expressing unboundedness in an enclosed plane that is bound by specific dimensions . . . .’

‘It is very clear to him that he is trying to express infinity, but it's also very clear to him that mathematics has something to offer,’ she said. 

Dr Gorini explained that in the regular division of the plane*, if you see even a checker board floor, the eye just imagines that it could go on for ever, because what you have done is take pieces—in this case squares—and you have just repeated the pieces over and over and over again. 

‘If you are familiar with Escher's art, you see a lot of that,’ she said. ‘You see lizards repeated over and over again. So the idea is that you have a shape that can fit together: a square works, a hexagon works, an equilateral triangle works—you just fit it together and repeat it.  

‘A floor cannot go on infinitely, but you can imagine it can, and what Escher did, which is totally amazing,’ she said, ‘is that he had all these shapes—lizards, or horsemen, or people, or birds, or fish—and he fitted them together so that they completely covered the plane, so you can see “Oh, if I trace this, I could go on forever.’' Even in one sheet of paper he has captured the idea of infinity.’ 

An artist can convey infinity just in a finite work, Dr Gorini said, and ‘the goal of mathematics is to take ideas about infinity and maybe make one formula, or one theorem, or one statement.  

‘As we continue [in her undergraduate course] we will keep seeing how mathematics expresses infinity; art expresses infinity, and both the mathematician and the artist can develop their own value of infinity by practising the Transcendental Meditation Technique.’ 

During the practice of Transcendental Meditation, the active mind settles down to quieter and quieter levels. At the quietest level, the mind experiences infinity itself. It's the actual experience of infinity. ‘It is awareness without the boundaries of a thought, without the boundaries of perception,’ Dr Gorini explained. 

‘Mathematicians and artists both experience that after meditation they are more familiar with infinity,’ she said. ‘They are familiar with infinity on a subjective level from their own direct experience, not just on the objective level of a theorem or a formula. 

‘Once a mathematician or an artist has that familiarity with infinity, they can express more of that infinite value in their work.’ 

© Copyright 2010 Global Good News®